Codeword a Day 2024 |

Sudoku a Day 2024 |

Wordsearch a Day 2024 |

Junior Codes Book |

Crossword a Day 2024 |

Kriss Kross a Day 2024 |

Mixed Puzzles Book |
Gift Ideas and Key Links
Popular Books:
Crossword a Day 2024

Codeword a Day 2024
Gift Ideas:

Mum's Book of Crosswords
Gift Ideas
Crossword Books
Codeword Books
Sudoku Books
Wordsearch Books
Brain Training
Kids Travel GamesDinosaur Puzzle Book
My first Word Search Book
Children's Fun Brain Training
Kids' Brain Training Puzzles
Colour By Number Maths
Kids' Number Kriss Kross
Children's Crosswords
Children's Codewords
Kids' Killer Sudoku
Under The Sea- Facts & Puzzles
Learning The Time
Children's Number Triangles
Children's Number Puzzles
Number Pyramids Puzzle Book
Mental Maths Book
Children's 6x6 Sudoku Book
Maths Squares Book
Gift Ideas 2020
Sudoku Puzzles
Christmas SudokuJigsawdoku Puzzle Book
Large Print Mixed Sudoku
16x16 Sudoku
25x25 Sudoku
12x12 Super Sudoku
Gigantic Sudoku
Mixed Sudoku
Fiendish Sudoku
Personalised Sudoku
Sudoku-London
Fillomino Puzzles
'X'mas Sudoku
Variety Sudoku
Valentine's Sudoku
Relaxing Sudoku
Sudoku a Day
Arrow Sudoku Book
Beginners 4x4 Sudoku Book
Calcudoku Book
Circle Sudoku Book
Consecutive Sudoku Book
Giant Sudoku Vol 1 & 2
Hypersudoku Book
Hidoku Book
Jigsaw Sudoku Vol 1 & 2
Killer Sudoku Vol 1 & 2
Killer Sudoku Large print
Large Print Sudoku Vol 1 & 2
Samurai Sudoku Vol 1 & 2
11 & 13 grid Samurai Sudoku
Sudoku 16x16 Vol 1 & 2
Sudoku 25x25 Sudoku Book
SuperSudoku 12x12 Book
Supreme Sudoku 15x15 Book
Sudoku X Book
Word Puzzles
Jumbo 20x20 Wordsearch PuzzlesLarge Print Arrow Word Puzzles
Kid's Word Fit Puzzles
Ultimate Crossword Mix
Bible Wordsearch Colouring
Giant Print Wordsearch
Word Definition Puzzles
Giant Print Crosswords
Word Trail Puzzles
Large Print Crosswords
Personalised Wordsearch
Large Print Kriss Kross
Kriss Kross Puzzles
Easy Themed Codewords Geography
Wordoku Puzzle Book
Large Print Wordsearch Book
Codewords Vol 1 & 2
Picture Wordsearch
Skeleton Crosswords Book
Word Ladders Book
Wordwheels Book
Logic / Number
Bridges PuzzlesNumber Fill Puzzles
Bathroom Mental Puzzles
Giant Kakuro
Magic Square Puzzles
ABC logic Puzzle Book
Battleships Book
Binary Puzzles Book
Binary Puzzles 12x12 Book
Large Print Code Words
Futoshiki
Hashi/Bridges Book
Kakuro Book
Minesweeper Puzzles Book
Number Cross Puzzle Book
Number Search Vol 1 & 2
Large Print Number Search Book
Number Squares Book
Sikaku Book
Simple Loop Book
Skeleton Crosswords vol 1 & 2
Space Maths Book
Puzzles For Your Pocket Books
Image / Visual
Dot-To-Dot:At The ZooUltimate Pets Adult Dot-to-dot
Large Print Adult Dot-to-dot
Adult Maze Puzzles-mixed
Kids' Maze Puzzles-mixed
Adult Dot-To-Dot
New Maze Puzzles
Children's Dot to Dots
Children's Maze Puzzles
Symbol Wordsearch Puzzles
COLOUR Hanjie Puzzle Book
Hanjie Puzzle Book
Perception Puzzles
Picture Mazes
Rebus Book
Summer Holiday Puzzle Book
Other Books
Sandwich SudokuKindness & Positivity Dot-To-Dot
Christmas Dot-To-Dot
Children's Personalised Birthday Story
Large Print Puzzle Book
Mother's Day Dot-To-Dot
The Gift Of Sudoku
Grandad's Quiz Book
Children's Halloween Puzzles
Dot-To-Dot Personalised
Calming Puzzles
Colouring Wordsearch
Sudoku and Crossword Diary 2017
Personalised Codeword
Personalised Wordsearch
Personalised Sudoku
Mother's & Father's Day Sudoku
Personalised Notebook
Notes & Puzzles
Grandad's Novelty Crosswords
Children's Notes & Puzzles
'X'mas Sudoku
Puzzle While You Wait
Grandad's Notes & Puzzles
Wedding Vow Renewal Puzzles
Grandad's Sudoku Puzzles
Easter Puzzles
St George's Day Puzzles
Mother's/Father's Day Puzzles
Valentine's Sudoku
Birthday Mixed Puzzles
Children's Personalised Book
Book of Christmas Puzzles
Personalised Family Puzzle Book
Birthday Sudoku Book
Occasion Books
Secret Santa Puzzle Book
Anniversary Sudoku Book
Calcudoku Book
|
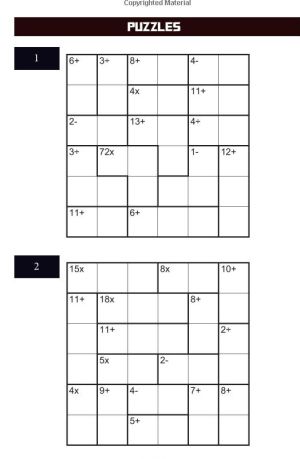
Welcome to this fantastic collection of 100 calcudoku puzzles.
All the puzzles are 6x6 in size, and puzzles vary in difficulty.
The rules of calcudoku are as follows: - Place the numbers from 1 - 6 exactly once in each row and column in the puzzle. - Bold-lined regions contain a sum. This might be a multiplication, division, subtraction or addition. The numbers in the bold-lined regions must be such as to make the sum valid. For instance, if the sum is '4+' and there are two cells in the bold-lined region, then the two numbers must sum to 4. - For division and subtraction sums, start with the largest number and then divide or subtract the other, smaller numbers from that as appropriate. For instance, in a region containing the numbers 3, 6 and 1 in any order, then if the symbol in that region is divide, then the total would be 2, because 6 divided by 3 divided by 1 is 2. Similarly for subtraction in this instance: 6 - 3 - 1 = 2. - Numbers are allowed to repeat within the bold-lined regions, as long as doing so doesn't break the rule that a number cannot repeat within a row or column. This means that bold-lined regions of two cells cannot contain repeat digits, since they of course are always contained within a single row or column. The book is available to purchase from Amazon.co.uk, Amazon.com and Amazon.eu. Please click the relevant link below to purchase this book via Amazon: If you're based in Europe but outside the UK, then this book is also available on the version of Amazon in your country. Tips On Solving CalcudokuLet's look at the second puzzle shown to the right, and some ideas on where to start solving it. We know that the numbers 1 - 6 appear once in each region: let's use this to narrow down some options. You'll often find that pencilmarks are essential in solving calcudoku, particularly as you get started with your solve.Look at the first sum - it is 15x from three squares. So we know that between the numbers 1,2,3,4,5,6 then there is only one combination that will multiply together to create that total: it is 1 x 3 x 5. So we know straight away that the only numbers left for the rest of the row are 2,4,6. Now, the next sum in the first row is 8x: we know that must be 4x2. That means that the final number in the row must be 6, and since that 6 is part of a sum of two squares to 10, then the square beneath it must contain a 4. So, we can see that just by narrowing down the options for the sums we can very quickly make progress in solving calcudoku puzzles. It is really all about spending a little time at the start looking for sums that only have one option, then noting those down as pencilmarks: being able to exclude those numbers from any other cell in the region is a powerful strategy that quickly helps you reduce the options elsewhere and start making progress with your solve. A quick scan of the grid will usually help with the above: numbers ending in odd numbers can be useful for multiplications and divisions. Look at the fourth row: there is a 5x from two squares, so we know that must be the 1 and 5 in that row taken care of. That means that the '2-' that is alongside it can't contain either 1 or 5. The options there without knowing anything were 6 and 4, 5 and 3, 4 and 2, 3 and 1. Note how two of those options are removed now, leaving 6 and 4 OR 4 and 2. This tells us that the 4 for the row must be placed in one of these two squares, so it definitely can't appear anywhere else in the row: useful information particularly when solving some of the harder calcudoku puzzles. Just be careful to remember that where not all squares in a bold-lined region are in the same row or column that numbers can repeat, so your strategies from killer sudoku won't always work. Do you have any particular method or solving strategies you find useful when solving calcudoku? Let us know and we'd be pleased to add them to this page!
Never tried a calcudoku puzzle? You can try a sample Calcudoku Online here. If you prefer to play puzzles online rather than in print, you can also play thousands of online puzzles with a membership to the Puzzle Connoisseur's Club.
Here is a video that explains the rules of calcudoku:
...and here is another that walks through the way to solve a calcudoku step-by-step: |

|
How to solve Jigsaw Sudoku
In our new series of videos, you can learn about new puzzle types and take part in quizzes. Why not have a watch?Been tempted by jigsaw sudoku but found it too tricky, or perhaps you've tried but got stuck? This video walks through the solve of a jigsaw (irregular) sudoku, and you can try the puzzle before you watch...
For individuals with comments, questions or ideas with regard to our puzzle books, then please use this Contact Form to drop us a line.