Codeword a Day 2026 |

Relaxing Dot to Dots |

Crossword a Day 2026 |

Junior Codes Book |

Quiz a Day 2026 |

Grandad's Crosswords |

Mixed Puzzles Book |
Gift Ideas and Key Links
Popular Books:

Gift Ideas:

Grandad's Book of Crosswords
Gift Ideas
Crossword Books
Codeword Books
Sudoku Books
Wordsearch Books
Brain Training
Kids Travel GamesDinosaur Puzzle Book
My first Word Search Book
Children's Fun Brain Training
Kids' Brain Training Puzzles
Colour By Number Maths
Kids' Number Kriss Kross
Children's Crosswords
Children's Codewords
Kids' Killer Sudoku
Under The Sea- Facts & Puzzles
Learning The Time
Children's Number Triangles
Children's Number Puzzles
Number Pyramids Puzzle Book
Mental Maths Book
Children's 6x6 Sudoku Book
Maths Squares Book
Gift Ideas 2020
Sudoku Puzzles
Christmas SudokuJigsawdoku Puzzle Book
Large Print Mixed Sudoku
16x16 Sudoku
25x25 Sudoku
12x12 Super Sudoku
Gigantic Sudoku
Mixed Sudoku
Fiendish Sudoku
Personalised Sudoku
Sudoku-London
Fillomino Puzzles
'X'mas Sudoku
Variety Sudoku
Valentine's Sudoku
Relaxing Sudoku
Sudoku a Day
Arrow Sudoku Book
Beginners 4x4 Sudoku Book
Calcudoku Book
Circle Sudoku Book
Consecutive Sudoku Book
Giant Sudoku Vol 1 & 2
Hypersudoku Book
Hidoku Book
Jigsaw Sudoku Vol 1 & 2
Killer Sudoku Vol 1 & 2
Killer Sudoku Large print
Large Print Sudoku Vol 1 & 2
Samurai Sudoku Vol 1 & 2
11 & 13 grid Samurai Sudoku
Sudoku 16x16 Vol 1 & 2
Sudoku 25x25 Sudoku Book
SuperSudoku 12x12 Book
Supreme Sudoku 15x15 Book
Sudoku X Book
Word Puzzles
Jumbo 20x20 Wordsearch PuzzlesLarge Print Arrow Word Puzzles
Kid's Word Fit Puzzles
Ultimate Crossword Mix
Bible Wordsearch Colouring
Giant Print Wordsearch
Word Definition Puzzles
Giant Print Crosswords
Word Trail Puzzles
Large Print Crosswords
Personalised Wordsearch
Large Print Kriss Kross
Kriss Kross Puzzles
Easy Themed Codewords Geography
Wordoku Puzzle Book
Large Print Wordsearch Book
Codewords Vol 1 & 2
Picture Wordsearch
Skeleton Crosswords Book
Word Ladders Book
Wordwheels Book
Logic / Number
Bridges PuzzlesNumber Fill Puzzles
Bathroom Mental Puzzles
Giant Kakuro
Magic Square Puzzles
ABC logic Puzzle Book
Battleships Book
Binary Puzzles Book
Binary Puzzles 12x12 Book
Large Print Code Words
Futoshiki
Hashi/Bridges Book
Kakuro Book
Minesweeper Puzzles Book
Number Cross Puzzle Book
Number Search Vol 1 & 2
Large Print Number Search Book
Number Squares Book
Sikaku Book
Simple Loop Book
Skeleton Crosswords vol 1 & 2
Space Maths Book
Puzzles For Your Pocket Books
Image / Visual
Dot-To-Dot:At The ZooUltimate Pets Adult Dot-to-dot
Large Print Adult Dot-to-dot
Adult Maze Puzzles-mixed
Kids' Maze Puzzles-mixed
Adult Dot-To-Dot
New Maze Puzzles
Children's Dot to Dots
Children's Maze Puzzles
Symbol Wordsearch Puzzles
COLOUR Hanjie Puzzle Book
Hanjie Puzzle Book
Perception Puzzles
Picture Mazes
Rebus Book
Summer Holiday Puzzle Book
Other Books
Sandwich SudokuKindness & Positivity Dot-To-Dot
Christmas Dot-To-Dot
Children's Personalised Birthday Story
Large Print Puzzle Book
Mother's Day Dot-To-Dot
The Gift Of Sudoku
Grandad's Quiz Book
Children's Halloween Puzzles
Dot-To-Dot Personalised
Calming Puzzles
Colouring Wordsearch
Sudoku and Crossword Diary 2017
Personalised Codeword
Personalised Wordsearch
Personalised Sudoku
Mother's & Father's Day Sudoku
Personalised Notebook
Notes & Puzzles
Grandad's Novelty Crosswords
Children's Notes & Puzzles
'X'mas Sudoku
Puzzle While You Wait
Grandad's Notes & Puzzles
Wedding Vow Renewal Puzzles
Grandad's Sudoku Puzzles
Easter Puzzles
St George's Day Puzzles
Mother's/Father's Day Puzzles
Valentine's Sudoku
Birthday Mixed Puzzles
Children's Personalised Book
Book of Christmas Puzzles
Personalised Family Puzzle Book
Birthday Sudoku Book
Occasion Books
Secret Santa Puzzle Book
Anniversary Sudoku Book
Book Of Battleships
|
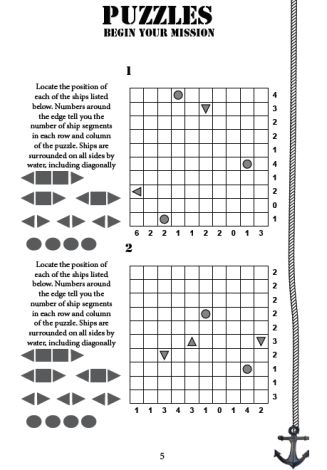
Battleships is a very absorbing logic puzzle that, although not often seen in publication, can be very satisfying and enjoyable to solve.
This book contains 100 all new battleship puzzles on a 10x10 grid. There are two puzzles per page, and there are full solutions at the back of the book. You can see the front cover for our battleships book to the right, along with an interior page below. Here are the rules of battleships puzzles:
Although the rules are quite simple, solving battleships puzzles can be a real challenge! There are amny subtle rules that you'll discover whilst you go through solving battleships puzzles. Each puzzle in this book has a single solution, and they get gradually harder as you work your way through the book. Be sure to cross off any cells that must contain water (as opposed to a ship segment) whilst solving the puzzle, and cross off any ships as you work out where they are in the grid - this will help you keep track of where you are in the solving process and the deductions that you make whilst solving. If you would like to try a few of the puzzles before buying this book, please click the link below: The book of battleships is available to purchase right now from Amazon.co.uk, Amazon.com and Amazon.eu. Please click the relevant link below to purchase this book via Amazon: If you're based in Europe but outside the UK, then this book is also available on the version of Amazon in your country.
We hope you have a fair wind behind your sails whilst tackling our fantastic fleet of battleships puzzles - do let us know how you get on, me hearties!
Battleship Solving StrategiesThere are lots of rules that you can use when solving battleships. Some who have struggled to solve all but the easy puzzles have asked for a couple of brief tips, so here goes:First, mark in the obvious: any rows or columns of 0 can be crossed off and marked as water. Next, look at the ships you are given. Are there any subs? These are ships marked as circles. You know that nothing around them can be a ship, so you can cross off all adjacent cells (including diagonally): this often gives you eight waters straight off. Then look at the larger ship segments: if there is orientation information available, then you can mark in at least one more square of the ship even if you don't know what type it is, and also mark in more water. The next thing to look at once you've done that is to see where each ships of each length can be placed. Typically it is best to start with the longest ship, though not necessarily, and see where it can be placed. There are often very few options for the longest ships. If there are a couple of options, then you might need to visualise the impact of each placement: does it lead to a contradiction whereby placing the ship in one location means that affected rows/columns could now not be completed as required? If there is a contradiction, then that placement can be marked off. Often you will not know exactly which squares are ship segments, but you will know that there are certain limits on where they go, or that one of a group of squares must contain a ship. This can often be used to mark in more water, particularly because of the diagonal constraint. And sometimes you will know, for instance, that there are only two regions in which the ships of length 3 can go but without being sure whereabouts in those two regions they are placed. This means that you now know that they CAN'T be placed anywhere else. If the four is already placed, this means that any other ships of length 2 you have that you thought might extend into a three ship can't extend, because then you would be placing too many three ships, and therefore they can be 'sealed off' with water and crossed off the list. As it can be seen, there are lots of rules both obvious and more subtle that can aid with solving harder battleship puzzles, and whilst with the easy and some of the medium you won't need them, as you get to some of the harder hard puzzles, then you will need to use a wider range of solving rules to reach the unique solution that exists for each puzzle. |

|
General Knowledge Quiz 2
In our new series of videos, you can learn about new puzzle types and take part in quizzes. Why not have a watch?This is our second general knowledge quiz. It's time to see how good your general knowledge is! We hope you enjoy having a go and seeing what score you'll get!
For individuals with comments, questions or ideas with regard to our puzzle books, then please use this Contact Form to drop us a line.