Consecutive Sudoku Book

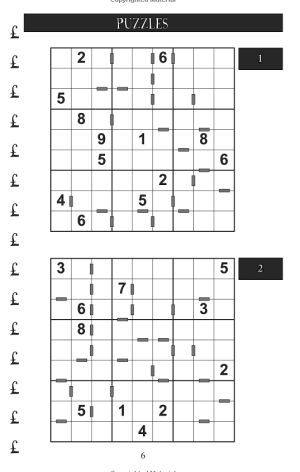
There are 100 puzzles in this book of consecutive sudoku, and the rules are simple: place the numbers from 1 - 9 once in each row, column and 3 x 3 box, and in accordance with the grey rectangles that appear between cells and tell you that the values in those cells are consecutive.

For instance, if there is a grey bar between two cells and one contains the number 3, then the cell next to it must contain either 2 or 4. Where the logic gets really interesting is where there are a run of consecutive cells in adjacent cells: this can often be used to reduce values surprisingly quickly.

All the 100 consecutive sudoku puzzles in this book have a unique solution that can be reached through the application of logic alone. There are full solutions at the back of the book so you can check your answers are correct or get inspiration if you hit a solving block.

If you haven't played these puzzles before but enjoy sudoku, then you should find these consecutive sudoku puzzles a refreshing and enjoyable change to the usual sudoku puzzles. So why not give this collection of puzzles a go?

If you would like to try a few of the puzzles before buying this book, please click the link below:

Consecutive Sudoku Sample

The Book of Consecutive Sudoku is available to purchase right now from Amazon.co.uk, Amazon.com and Amazon.eu. Please click the relevant link below to purchase this book via Amazon:

Consecutive Sudoku Solving Strategies

First, we should say that with these consecutive sudoku puzzles, you DON'T need to use the inverse rule: eg that if two squares are not marked as consecutive, then they can't be consecutive: nowhere in the rules for these consecutive sudoku puzzles is it stated that all instances of consecutive values are shown. As a point of fact in the books produced so far they are, but you will never need to use this fact to solve any of the puzzles.

With that out of the way, onto the strategy. The key is to go through the puzzle at the start and look at all consecutive markers, and see what deductions you can make from these. Go through and write in all possible values where you know them. At the start you should pay particular attention to consecutive markers next to a square that has a value in it, as this instantly narrows the range to 2 or possibly just 1 option.

Look at puzzle 2 to the right. Loko at the 7 in row 2, we instantly know that the square to the right of it must be 6 or 8. Then in row 3, the square to the right of the 6 must be 5 or 7; the square above the 3 in that row must be 2 or 1. Keep working through writing these easy pencilmark deductions in. Now you might have enough information to use sudoku solving rules to make progress. If not, then you can also look for chains of consecutive cells and the logic that comes with those to try and make deductions.

There are two many rules to look into where cells chain together and the deductions you can make in a short treatment like this. We'll just look at one simple piece of logic unique to the consecutive cells to illustrate the point that there are many subtle rules they introduce to the solving logic: look at the middle square in box 4 (the square underneath the only given 8 in the second puzzle). Note that it is consecutive in value to TWO squares: the one beneath it, and to its right. We instantly know when we see this, and the two other squares are in the same region, that the value of the square cannot be either 1 or 9. Can you see why this is the case?

Here's a video that explains the rules of consecutive sudoku: