Logic Puzzles for Adults |

Mixed Puzzles Book |

Grandad's Crosswords |

Arrow Word Puzzles |

Relaxing Dot to Dots |

Codeword a Day 2024 |

Crossword a Day 2024 |
Gift Ideas and Key Links
Popular Books:
Crossword a Day 2024

Codeword a Day 2024
Gift Ideas:

Grandad's Book of Crosswords
Gift Ideas
Crossword Books
Codeword Books
Sudoku Books
Wordsearch Books
Brain Training
Kids Travel GamesDinosaur Puzzle Book
My first Word Search Book
Children's Fun Brain Training
Kids' Brain Training Puzzles
Colour By Number Maths
Kids' Number Kriss Kross
Children's Crosswords
Children's Codewords
Kids' Killer Sudoku
Under The Sea- Facts & Puzzles
Learning The Time
Children's Number Triangles
Children's Number Puzzles
Number Pyramids Puzzle Book
Mental Maths Book
Children's 6x6 Sudoku Book
Maths Squares Book
Gift Ideas 2020
Sudoku Puzzles
Christmas SudokuJigsawdoku Puzzle Book
Large Print Mixed Sudoku
16x16 Sudoku
25x25 Sudoku
12x12 Super Sudoku
Gigantic Sudoku
Mixed Sudoku
Fiendish Sudoku
Personalised Sudoku
Sudoku-London
Fillomino Puzzles
'X'mas Sudoku
Variety Sudoku
Valentine's Sudoku
Relaxing Sudoku
Sudoku a Day
Arrow Sudoku Book
Beginners 4x4 Sudoku Book
Calcudoku Book
Circle Sudoku Book
Consecutive Sudoku Book
Giant Sudoku Vol 1 & 2
Hypersudoku Book
Hidoku Book
Jigsaw Sudoku Vol 1 & 2
Killer Sudoku Vol 1 & 2
Killer Sudoku Large print
Large Print Sudoku Vol 1 & 2
Samurai Sudoku Vol 1 & 2
11 & 13 grid Samurai Sudoku
Sudoku 16x16 Vol 1 & 2
Sudoku 25x25 Sudoku Book
SuperSudoku 12x12 Book
Supreme Sudoku 15x15 Book
Sudoku X Book
Word Puzzles
Jumbo 20x20 Wordsearch PuzzlesLarge Print Arrow Word Puzzles
Kid's Word Fit Puzzles
Ultimate Crossword Mix
Bible Wordsearch Colouring
Giant Print Wordsearch
Word Definition Puzzles
Giant Print Crosswords
Word Trail Puzzles
Large Print Crosswords
Personalised Wordsearch
Large Print Kriss Kross
Kriss Kross Puzzles
Easy Themed Codewords Geography
Wordoku Puzzle Book
Large Print Wordsearch Book
Codewords Vol 1 & 2
Picture Wordsearch
Skeleton Crosswords Book
Word Ladders Book
Wordwheels Book
Logic / Number
Bridges PuzzlesNumber Fill Puzzles
Bathroom Mental Puzzles
Giant Kakuro
Magic Square Puzzles
ABC logic Puzzle Book
Battleships Book
Binary Puzzles Book
Binary Puzzles 12x12 Book
Large Print Code Words
Futoshiki
Hashi/Bridges Book
Kakuro Book
Minesweeper Puzzles Book
Number Cross Puzzle Book
Number Search Vol 1 & 2
Large Print Number Search Book
Number Squares Book
Sikaku Book
Simple Loop Book
Skeleton Crosswords vol 1 & 2
Space Maths Book
Puzzles For Your Pocket Books
Image / Visual
Dot-To-Dot:At The ZooUltimate Pets Adult Dot-to-dot
Large Print Adult Dot-to-dot
Adult Maze Puzzles-mixed
Kids' Maze Puzzles-mixed
Adult Dot-To-Dot
New Maze Puzzles
Children's Dot to Dots
Children's Maze Puzzles
Symbol Wordsearch Puzzles
COLOUR Hanjie Puzzle Book
Hanjie Puzzle Book
Perception Puzzles
Picture Mazes
Rebus Book
Summer Holiday Puzzle Book
Other Books
Sandwich SudokuKindness & Positivity Dot-To-Dot
Christmas Dot-To-Dot
Children's Personalised Birthday Story
Large Print Puzzle Book
Mother's Day Dot-To-Dot
The Gift Of Sudoku
Grandad's Quiz Book
Children's Halloween Puzzles
Dot-To-Dot Personalised
Calming Puzzles
Colouring Wordsearch
Sudoku and Crossword Diary 2017
Personalised Codeword
Personalised Wordsearch
Personalised Sudoku
Mother's & Father's Day Sudoku
Personalised Notebook
Notes & Puzzles
Grandad's Novelty Crosswords
Children's Notes & Puzzles
'X'mas Sudoku
Puzzle While You Wait
Grandad's Notes & Puzzles
Wedding Vow Renewal Puzzles
Grandad's Sudoku Puzzles
Easter Puzzles
St George's Day Puzzles
Mother's/Father's Day Puzzles
Valentine's Sudoku
Birthday Mixed Puzzles
Children's Personalised Book
Book of Christmas Puzzles
Personalised Family Puzzle Book
Birthday Sudoku Book
Occasion Books
Secret Santa Puzzle Book
Anniversary Sudoku Book
Hashi/Bridges
|
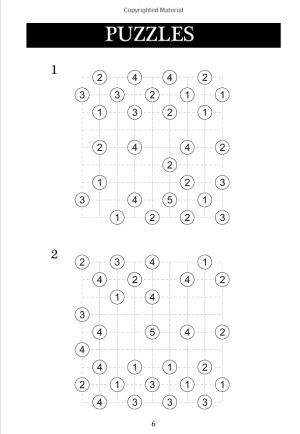
Welcome to this fantastic collection of 100 bridges puzzles.
The book contains 50 grids that are 9 x 9 in size, and are ideal for beginners, followed by 50 grids at a much larger 15 x 15 grid size, ideal for those who are experienced with bridges puzzles already, or have worked through the smaller puzzles. Here are the rules of bridges puzzles (also known as hashi puzzles). - The grid contains lots of circled cells containing numbers. These are known as islands. - Islands are connected by bridges. The number inside an island tells you how many bridges it has to other islands. - There cannot be more than two bridges between any pair of islands. Bridges must be either vertical or horizontal (not diagonal). Bridges cannot cross each other. - At the end of the puzzle once all bridges are drawn in, it must be possible to move from any island to any other island in the puzzle by walking across bridges from island to island. In other words, there are no isolated groups of islands. If you are uncertain, take a look at a couple of the solutions quickly to see what a valid solution looks like and how the bridges are connected.
If you would like to try a few of the puzzles before buying this book, please click the link below: The book is available to purchase from Amazon.co.uk, Amazon.com and Amazon.eu. Please click the relevant link below to purchase this book via Amazon: If you're based in Europe but outside the UK, then this book is also available on the version of Amazon in your country. Hashi / Bridges Solving TipsIf you're reading this page, the chances are good that it's because you are a hashi fan and therefore good at solving the puzzles. But for those who are intrigued by this game and haven't played it before, here are some solving tips for you:Firstly, look for instances where a 1 island can go to another 1 island, and put a cross between those two. That's because they can't join together, because if they did they would form an isolated set of just two islands. Similary, with a '2' remember that it can't double-link to another '2'. So if you see a set of bridges whereby a '2' bridge has two neighbours, one of which is another '2' bridge, then you know that it must have AT LEAST one link to the other neighbour that isn't the '2'. This can be very helpful when solving these puzzles. The simplest of all tips is to look at the corners and the edges for high-value islands, as typically at least some bridges for these can be drawn in. Remember the basic rule: there can be no more than two bridges between islands. So an island with a value of '7' with the maximum of four possible neighbours must have at least one link to each, which can be drawn in: that's because the only combination for a '7' is to have both bridges with three islands, and one with another. Of course, an '8' island can be drawn in instantly: it must have double bonds in all directions: for this reason an '8' is rarely seen in bridges or hashi but you do come across it from time to time. Generally when solving puzzles working out where an island must bond, and using the simple rules about non-isolation are all you will need, together with good accounting. Typically this means putting a small cross between islands you know that can't bond to each other, and also it is good practice to put a line through an island when you have placed all its bridges: as miscounting is one of the most common mistakes made when solving bridges and can be very frustrating particularly with the larger puzzles. If you do get stuck, then bear in mind with some bridges puzzles you will need to use more difficult isolation rules: for instance thinking 'if these two islands connect via a bridge then this clump of ten islands will then be isolated from the rest of the grid'. Rest assured that with our puzzles there is a unique logical solution: you will not need to do anything more difficult than the rule just mentioned of looking at possible bridges between islands and working out which will lead to isolation: you won't need any if this and if this type logic. |

|
How to Solve Futoshiki Puzzles
In our new series of videos, you can learn about new puzzle types and take part in quizzes. Why not have a watch?In this video we look at the rules of futoshiki and how they work. We examine the greater than and less than signs that are the key addition to standard sudoku rules. Take a look if you're tempted to have a go at this puzzle type...
For individuals with comments, questions or ideas with regard to our puzzle books, then please use this Contact Form to drop us a line.